Sstrhsrtj

出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。記事の信頼性向上にご協力をお願いいたします。（2013年3月）

縦と横の長さの比の値が黄金比の近似値1:1.618である長方形。

黄金比（おうごんひ、英語: golden ratio）は、

1:1+52{displaystyle 1:{frac {1+{sqrt {5}}}{2}}}

の比である。近似値は1:1.618、約5:8。

線分を a, b の長さで 2 つに分割するときに、a : b = b : (a + b) が成り立つように分割したときの比 a : b のことであり、最も美しい比とされる。貴金属比の1つ（第1貴金属比）。

黄金比において

1+52{displaystyle {frac {1+{sqrt {5}}}{2}}}

は、二次方程式 x² − x − 1 = 0 の正の解であり、これを黄金数（おうごんすう、英語: golden number）という。しばしばギリシア文字の φ（ファイ）で表されるが、τ（タウ）を用いる場合もある。

ϕ=1+52=1.6180339887…{displaystyle phi ={frac {1+{sqrt {5}}}{2}}=1.6180339887ldots }

黄金数には，次のような性質がある。

ϕ2=ϕ+1=2.6180339887…{displaystyle phi ^{2}=phi +1=2.6180339887ldots }

1/ϕ=ϕ−1=0.6180339887…{displaystyle 1/phi =phi -1=0.6180339887ldots }

黄金比は中末比（ちゅうまつひ）や外中比（がいちゅうひ）とも呼ばれる。a : b = b : (a + b) が成り立つとき、a を末項（まっこう）、b を中項（ちゅうこう）という。

性質

黄金長方形（辺の長さの比が黄金比になる四角形）の黄金分割。黄金長方形から短辺を一辺とする正方形を取り除くと、残る部分はまた黄金長方形となる。これを繰り返すと、黄金長方形は無限個の正方形で埋め尽くされる。

黄金長方形においては、長辺と短辺の比が、短辺と「長辺と短辺の差」の比と等しくなっている。

黄金長方形の長辺および「長辺と短辺の差」のそれぞれと同じ長さの辺をもつ長方形(図中の右上の赤色で示す領域)の面積は、同一の黄金長方形の短辺と同じ長さの辺をもつ正方形(図中の左下の赤色で示す領域)の面積と等しい。（図中の２つの青枠で示される長方形は互いに合同な黄金長方形）

幅と高さが１とφの黄金長方形について、その幅・高さ・対角線で構成される直角三角形を用い、φと(φ−1)の積が1(斜線の正方形および長方形は互いに同じ面積)となり、また、対角線と同じ長さの辺を持つ正方形の面積がΦと√5の積(赤色の正方形及び長方形は互いに同じ面積)となることを表した図。

黄金長方形については、長辺：短辺＝短辺：（長辺－短辺）＝（長辺＋短辺）：長辺が成り立つ。

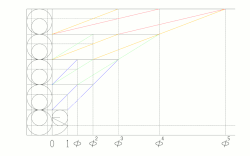
1,φ,φ²,φ³,φ⁴,φ⁵,...の等比数列の ３番目以降の項がそれぞれ直前の２項の和となる性質を幾何学的に表した図。青・緑・黄・赤の直線について、同色のものは互いに平行となっている。

−1+52:1=1:1+52=1+52:3+52{displaystyle {{-1+{sqrt {5}}} over 2}:1=1:{{1+{sqrt {5}}} over 2}={{1+{sqrt {5}}} over 2}:{{3+{sqrt {5}}} over 2}}

上式を小数の近似値で表示すると、0.618 : 1 ≒ 1 : 1.618 ≒ 1.618 : 2.618 となる。

黄金数は次のような美しい連分数表示をもつ。

ϕ=1+11+11+11+1⋱=[1;1,1,1,1,…]{displaystyle phi =1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{ddots }}}}}}}}=[1;1,1,1,1,ldots ]}

次のような表示ももつ。

ϕ−1=[0;1,1,1,…]=0+11+11+11+⋱{displaystyle phi ^{-1}=[0;1,1,1,ldots ]=0+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+ddots }}}}}}}

ϕ−1=ϕ−1=−1+52=0.6180339887…{displaystyle phi ^{-1}=phi -1={frac {-1+{sqrt {5}}}{2}}=0.6180339887ldots ,}

ϕ=1+1+1+1+…{displaystyle phi ={sqrt {1+{sqrt {1+{sqrt {1+{sqrt {1+{sqrt {ldots }}}}}}}}}}}

ϕ=138+∑n=0∞(−1)(n+1)(2n+1)!(n+2)!n!4(2n+3){displaystyle phi ={frac {13}{8}}+sum _{n=0}^{infty }{frac {(-1)^{(n+1)}(2n+1)!}{(n+2)!n!4^{(2n+3)}}}}

三角関数を使うと次のように表すことができる。

ϕ=2cos⁡π5=2cos⁡36∘{displaystyle phi =2cos {pi over 5}=2cos 36^{circ }}

ϕ=2sin⁡3π10=2sin⁡54∘{displaystyle phi =2sin {{3pi } over 10}=2sin 54^{circ }}

ϕ=−2sin⁡(666∘){displaystyle phi =-2sin(666^{circ })}

ϕ=1+2sin⁡π10=1+2sin⁡18∘{displaystyle phi =1+2sin {pi over 10}=1+2sin 18^{circ }}

ϕ=1+2cos⁡2π5=1+2cos⁡72∘{displaystyle phi =1+2cos {{2pi } over 5}=1+2cos 72^{circ }}

ϕ=12csc⁡π10=12csc⁡18∘{displaystyle phi ={1 over 2}csc {pi over 10}={1 over 2}csc 18^{circ }}

ϕ−1=2sin⁡π10=2sin⁡18∘{displaystyle phi ^{-1}=2sin {pi over 10}=2sin 18^{circ }}

ϕ−1=2cos⁡2π5=2cos⁡72∘{displaystyle phi ^{-1}=2cos {{2pi } over 5}=2cos 72^{circ }}

指数関数を使うと次のように表すことができる。

ϕ=eπi5+e−πi5{displaystyle phi =e^{{pi i} over 5}+e^{{-pi i} over 5}}

フィボナッチ数列の隣り合う 2 項の比は黄金比に収束する。また、 1, φ, φ², φ³, φ⁴, ... という等比数列を考えたとき、1 + φ = φ² を利用すると

φ = φ,

φ² = φ + 1,

φ³ = 2φ + 1,

φ⁴ = 3φ + 2,

φ⁵ = 5φ + 3,

φ⁶ = 8φ + 5,

...

となり、係数にフィボナッチ数列が出現する。フィボナッチ数列の第 n 項を F_n とすると、φⁿ は次のようになる。

φⁿ = F_nφ + F_n-1

直径の比が、

ϕ−ϕ:1:ϕ+ϕ{displaystyle {phi -{sqrt {phi }}}:1:{phi +{sqrt {phi }}}}

である３つの円が互いに外接する時、その３つの円の全てに外接する円を２つ描くことが出来る。

それらを合わせた５つの円の直径の比は、

(ϕ−ϕ)2:ϕ−ϕ:1:ϕ+ϕ:(ϕ+ϕ)2{displaystyle ({phi -{sqrt {phi }}})^{2}:{phi -{sqrt {phi }}}:1:{phi +{sqrt {phi }}}:({phi +{sqrt {phi }}})^{2}}

である。

黄金比で長さを分けることを黄金比分割または黄金分割という。

幾何学的には正五角形や五芒星（星形：☆）から容易に得ることができる。正五角形の一辺と対角線の比、五芒星を構成する線分と頂点を結ぶ線分の比は、黄金比となる。

歴史

ジャック＝ルイ・ダヴィッドの『レカミエ像』（1800年）。構図が安定して見えるのは、夫人の横たわる姿が黄金比の長方形に収まるように構成されているからだという。

• 伝承では、古代ギリシアの彫刻家ペイディアス (Φειδίας) が初めて使ったといわれる。黄金数の記号φは彼の頭文字であるが、使われ始めたのは20世紀である。なお、τはギリシア語の「分割」に由来し、やはり20世紀に使われ始めた。


• 
  レオナルド・ダ・ヴィンチも発見していた記録が残っている。


• 「黄金比」という用語が文献上に初めて登場したのは1835年刊行のドイツの数学者マルティン・オーム（オームの法則で有名なゲオルク・ジーモン・オームの弟）の著書『初等純粋数学』。また、1826年刊行の初版にはこの記載がないことから、1830年頃に誕生したと考えられる。


• 『ユークリッド原論』では第6巻の定義3で外中比の定義が記されている。


• 『ユークリッド原論』の第6巻の命題30で「与えられた線分を外中比に分ける作図法」が記されている。

黄金比の近似値

1:1.

6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362 1076738937 6455606060 5921658946 6759551900 4005559089 ･･････(オンライン整数列大辞典の数列 A001622)

現在の用途

黄金比は、名刺を初め、様々なカード類の縦横比にも利用されることが多い^[要出典]。

ディスプレイのアスペクト比には、WQXGA（解像度2560x1600）、WUXGA（同1920x1200）など、黄金比に近い8:5（16:10）のものもある。

作図

最も簡単な作図方法は下記の通り。

1. 正方形 abcd を描く。


2. 辺 bc の中点 o を中心に、コンパスなどを用いて線分 oa または od を半径とした円を描く。


3. 2で描いた円と辺 bc の延長線との交点を e とし、長方形abefを描く。


4. この時の長方形abefが、黄金比となる。

その他

直径同士の比が黄金比となる２つの円（いずれも正円であること）につき、小さい円が大きい円の右端で外接している場合、両円の中心を通る直線を軸に対称な両円に共通する２本の接線の交点と小さい円の右端との距離は大きい円の直径と等しくなっている。

この節は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。（2012年12月）

黄金比はパルテノン神殿やピラミッドといった歴史的建造物や美術品の中に見出すとされてきたが、これらは後付けの都市伝説であるものが含まれる。一方で、意図的に黄金比を意識して創作した芸術家も数多い^[1]。

長方形は縦と横との関係が黄金比になるとき、安定した美感を与えるという説がある。これはグスタフ・フェヒナーの1867年の実験を論拠としている。しかし、フェヒナーの実験の解釈については肯定的もしくは否定的な様々な見解がある。1997年に国際経験美学会誌の黄金分割特集では、この実験結果を「永遠に葬るもの」とする見解が掲載された。また類似の（すなわち、同様に根拠が極めてあやしい）安定した比とされるものに白銀比がある^[2]。

自然界に存在する植物の葉脈や巻き貝の断面図など対数螺旋では無いが黄金比（に似通った）の例として度々挙げられる。工学分野では、自動車ではスポーツカーやクロカン、セミトレーラー用トラクタや軽トラックのトレッド（輪距）とホイールベース（軸距）の関係が黄金比に近い。具体的には 普通乗用車であれば1,500 mm 程度のトレッドに対し、ホイールベースが2,400 mm 前後とやや短い値となる。これは、いずれの車種においても旋回性能が重要視されるためである。

黄金比は美容外科にても用いられ、身体において、足底から臍（へそ）までの長さと、臍から頭頂までの長さの比が黄金比であれば美しいとされることがある。また、顔面の構成要素である目、鼻、口などの長さや間隔、細かな形態も黄金比に合致すれば美しいと宣伝などで謳われている。

参考文献

• ハンス・ヴァルサー『黄金分割』日本評論社 ISBN 4535783470
  


• R.A.ダンラップ『黄金比とフィボナッチ数』日本評論社 ISBN 4535783705
  


• 中村滋『フィボナッチ数の小宇宙（ミクロコスモス）―フィボナッチ数、リュカ数、黄金分割』日本評論社 ISBN 4535782814
  


• 佐藤修一『自然にひそむ数学―自然と数学の不思議な関係』講談社ブルーバックス ISBN 406257201X
  


• アルプレヒト・ボイテルスパッヒャー、ベルンハルト・ペトリ『黄金分割―自然と数理と芸術と』共立出版 ISBN 4320017811
  


• 
  高木貞治『数学小景』岩波現代文庫 ISBN 4006000812
  


• 『ユークリッド原論（縮刷版）』共立出版 ISBN 4320015134
  


• 関隆志『古代アッティカ杯―ギリシア美術の比例と装飾の研究』 ISBN 4805505761
  


• Hrant Arakelian. Mathematics and History of the Golden Section, Logos 2014, ISBN 978-5-98704-663-0 (rus.).

関連項目

• 黄金螺旋


• 黄金進法


• 黄金分割探索


• 黄金三角形


• 黄金角


• フィボナッチ数


• 
  貴金属比
  
  
  
  • 白銀比
  
  
  • 青銅比
  
  
  
  


• 数学的な美

外部リンク

• Weisstein, Eric W. "Golden Ratio". MathWorld（英語）..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}


• 
  Golden Ratio - Wolfram Alpha
  


• 黄金比の色々―黄金比を具体例や図形でわかりやすく解説したサイト

この項目は、代数学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（プロジェクト:数学／Portal:数学）。