Sstrhsrtj

数学におけるヒルベルト空間（ヒルベルトくうかん、英: Hilbert space）は、ダフィット・ヒルベルトにその名を因む、ユークリッド空間の概念を一般化したものである。これにより、二次元のユークリッド平面や三次元のユークリッド空間における線型代数学や微分積分学の方法論を、任意の有限または無限次元の空間へ拡張して持ち込むことができる。ヒルベルト空間は、内積の構造を備えた抽象ベクトル空間（内積空間）になっており、そこでは角度や長さを測るということが可能である。ヒルベルト空間は、さらに完備距離空間の構造を備えている（極限が十分に存在することが保証されている）ので、その中で微分積分学がきちんと展開できる。

ヒルベルト空間は、典型的には無限次元の関数空間として、数学、物理学、工学などの各所に自然に現れる。そういった意味でのヒルベルト空間の研究は、20世紀冒頭10年の間にヒルベルト、シュミット、リースらによって始められた。ヒルベルト空間の概念は、偏微分方程式論、量子力学、フーリエ解析（信号処理や熱伝導などへの応用も含む）、熱力学の研究の数学的基礎を成すエルゴード理論などの理論において欠くべからざる道具になっている。これら種々の応用の多くの根底にある抽象概念を「ヒルベルト空間」と名付けたのは、フォン・ノイマンである。ヒルベルト空間を用いる方法の成功は、関数解析学の実りある時代のさきがけとなった。古典的なユークリッド空間はさておき、ヒルベルト空間の例としては、自乗可積分関数の空間 L²、自乗総和可能数列の空間 ℓ²、超関数からなるソボレフ空間 H^s、正則関数の成すハーディ空間 H² などが挙げられる。

ヒルベルト空間論の多くの場面で、幾何学的直観は重要である。例えば、三平方の定理や中線定理（の厳密な類似対応物）は、ヒルベルト空間においても成り立つ。より深いところでは、部分空間への直交射影（例えば、三角形に対してその「高さを潰す」操作の類似対応物）は、ヒルベルト空間論における最適化問題やその周辺で重要である。ヒルベルト空間の各元は、平面上の点がそのデカルト座標（直交座標）によって特定できるのと同様に、座標軸の集合（正規直交基底）に関する座標によって一意的に特定することができる。このことは、座標軸の集合が可算無限であるときには、ヒルベルト空間を自乗総和可能な無限列の集合と看做すことも有用であることを意味する。ヒルベルト空間上の線型作用素は、ほぼ具体的な対象として扱うことができる。条件がよければ、空間を互いに直交するいくつかの異なる要素に分解してやると、線型作用素はそれぞれの要素の上では単に拡大縮小するだけの変換になる（これはまさに線型作用素のスペクトルを調べるということである）。

定義と導入

動機付けとなる例

最もよく知られたヒルベルト空間の例の一つは、三次元の空間ベクトル全体の成すユークリッド空間 R³ にドット積を考えたものであろう。二つのベクトル x, y のドット積 x · y は実数を与える。x と y がデカルト座標系であらわされているときには、ドット積は

(x1,x2,x3)⋅(y1,y2,y3):=x1y1+x2y2+x3y3{displaystyle (x_{1},x_{2},x_{3})cdot (y_{1},y_{2},y_{3}):=x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}}

として定まる。このドット積は、条件

1. 
   対称性: x · y = y · x.


2. 第一引数に関する線型性: (ax₁ + bx₂) · y = ax₁ · y + bx₂ · y （a, b は任意のスカラー、x₁, x₂, y は任意のベクトル）


3. 
   正定値性: 任意のベクトル x に対して x · x ≥ 0, 等号成立は x = 0 のとき、かつそのときに限る。

を満足する。

このドット積のように、上記三つの性質を満足するベクトルの二項演算を（実）内積と呼び、そのような内積を備えたベクトル空間は（実）内積空間と呼ばれる。任意の有限次元内積空間は、ヒルベルト空間でもある。ユークリッド幾何学に関わるドット積の基本的な特徴というのは、ベクトルの長さ（ノルム）‖x‖ と二つのベクトル x, y の間の角度 θ の両方が

x⋅y=‖x‖‖y‖cos⁡θ{displaystyle mathbf {x} cdot mathbf {y} =|mathbf {x} |,|mathbf {y} |,cos theta }

なる式が成立するという意味でドット積と関連付けられることである。
ユークリッド空間における多変数微分積分学は極限が計算できること、および極限の存在を結論付ける有用な判定法を持つことに支えられている。R³ のベクトルを項とする級数

∑n=0∞xn{displaystyle sum _{n=0}^{infty }mathbf {x} _{n}}

は、そのノルムの和（これは実数を項とする通常の級数）が

∑k=0∞‖xk‖<∞{displaystyle sum _{k=0}^{infty }|mathbf {x} _{k}|<infty }

なる条件を満たすとき、絶対収束するという^[1]。スカラー項級数の場合と全く同じく、絶対収束するベクトル項級数は

‖L−∑k=0Nxk‖→0as N→∞{displaystyle left|mathbf {L} -sum _{k=0}^{N}mathbf {x} _{k}right|to 0quad {text{as }}Nto infty }

なる意味で、このユークリッド空間の適当な極限ベクトル L に収束する。このような性質（絶対収束級数は通常の意味でも収束する）は、ユークリッド空間の完備性 (completeness) として表される。

定義

H がヒルベルト空間であるとは、H は実または複素内積空間であって、さらに内積によって誘導される距離関数に関して完備距離空間をなすことを言う^[2]。ここで、H が複素内積空間であるというのは、H は複素線型空間であって、その上に内積、即ち H の元の対 x, y に複素数 ⟨x,y⟩ を対応させる写像であって、条件

1. 
   ⟨y,x⟩ は ⟨x,y⟩ の複素共役である：
   ⟨y,x⟩=⟨x,y⟩¯.{displaystyle langle y,xrangle ={overline {langle x,yrangle }}.}
   
   


2. 
   ⟨x,y⟩ は第一引数に関して線型である^[3]： 任意の複素数 a, b に対して
   ⟨ax1+bx2,y⟩=a⟨x1,y⟩+b⟨x2,y⟩.{displaystyle langle ax_{1}+bx_{2},yrangle =alangle x_{1},yrangle +blangle x_{2},yrangle .}
   
   


3. 内積 ⟨•, •⟩ は正定値である：
   ⟨x,x⟩≥0{displaystyle langle x,xrangle geq 0}
   かつ等号成立は x = 0 と同値。

を満たすものが存在することをいう。条件の 1 と 2 を併せると、複素内積は第二引数に関して反線型 (antilinear) となることが従う。即ち、

⟨x,ay1+by2⟩=a¯⟨x,y1⟩+b¯⟨x,y2⟩{displaystyle langle x,ay_{1}+by_{2}rangle ={bar {a}}langle x,y_{1}rangle +{bar {b}}langle x,y_{2}rangle }

が成り立つ。実内積空間も同様に定められ（H が実線型空間であることと、内積が実数値であることとが違うだけである）、この場合の内積は双線型（各引数について線型）になる。

内積 ⟨•, •⟩ によって定義されるノルム

‖x‖:=⟨x,x⟩{displaystyle |x|:={sqrt {langle x,xrangle }}}

は実数値関数であり、このノルムを用いて H の2点 x, y 間の距離が

d(x,y):=‖x−y‖=⟨x−y,x−y⟩{displaystyle d(x,y):=|x-y|={sqrt {langle x-y,x-yrangle }}}

と定められる。これが距離であるというのは、(1)「x と y に関して対称」で、(2)「x と x 自身との距離は 0 に等しく、かつそれ以外のときは x と y との距離は必ず正」で、(3)「三角不等式

d(x,z)≤d(x,y)+d(y,z){displaystyle d(x,z)leq d(x,y)+d(y,z)}

を満たす、即ち三角形 xyz の一辺の長さは他の二辺の長さの和を超えない」という三性質を満たすことを意味する。
三つ目の性質は、突き詰めればより基本的なコーシー・シュヴァルツの不等式

|⟨x,y⟩|≤‖x‖‖y‖{displaystyle |langle x,yrangle |leq |x|,|y|}

（ただし等号成立は x, y の線型独立性と同値）からの帰結である。

このようにして定義される距離関数に関して、任意の内積空間は距離空間となる。内積空間のことを前ヒルベルト空間 (pre-Hilbert space) と呼ぶこともある^[4]。距離空間として完備であるような任意の前ヒルベルト空間は、ヒルベルト空間になる。完備性は、H 内の列に対するコーシーの判定法（英語版）の形で表すことができる。即ち、前ヒルベルト空間 H が完備となるのは、任意のコーシー列がノルムに関する意味で H 内の元に収束することである。完備性は、次のような条件

ベクトル項級数 ∑∞
k=0  u_k が

∑k=0∞‖uk‖<∞{displaystyle sum _{k=0}^{infty }|u_{k}|<infty }

なる意味で絶対収束するならば、もとの級数は（部分和が H の元に収束するという意味で） H において収束する。

によっても特徴付けることができる。

完備なノルム空間であるという点で、定義によりヒルベルト空間はバナッハ空間でもある。これらは位相線型空間であり、開集合や閉集合といった位相的概念を定めることができる。特に重要になるのが、ヒルベルト空間の閉部分空間の概念である。完備距離空間の閉部分集合は（そこへ距離を制限すれば）それ自身完備距離空間となるから、ヒルベルト空間の閉部分空間は（そこへ内積を制限するとき）それ自身ヒルベルト空間をなす。

もう少し自明でない例

複素数を項とする無限数列 z = (z₁, z₂, …) で級数

∑n=1∞|zn|2{displaystyle sum _{n=1}^{infty }|z_{n}|^{2}}

が収束するようなもの（自乗総和可能な無限複素数列）全体の成す数列空間を ℓ² で表す。ℓ² 上の内積はエルミート積として

⟨z,w⟩=∑n=1∞znw¯n{displaystyle langle mathbf {z} ,mathbf {w} rangle =sum _{n=1}^{infty }z_{n}{bar {w}}_{n}}

で定義される。この右辺の級数が収束することはコーシー・シュヴァルツの不等式からの帰結である。

空間 ℓ² の完備性は「ℓ² の元からなる級数が（ノルムの意味で）絶対収束するならば必ず、その級数が ℓ² の何らかの元に収束する」ことを示せば言える。このことの証明は解析学の初歩であり、この空間の元からなる級数は複素数（あるいは有限次元ベクトル空間のベクトル）からなる級数と同程度容易に扱うことができる^[5]。

歴史

ダフィット・ヒルベルト

ヒルベルト空間が開発される以前にも、数学や物理学においてユークリッド空間を一般化する別な概念が知られていた。特に、19世紀の終わりに掛けていくつかの流れの中から抽象線型空間の概念が獲得される^[6]。これは、その元同士の加法と（実数や複素数のような）スカラーによる乗法とを備えた空間のことを指すのであって、必ずしも物理的な系における運動量や位置といった「幾何学的な」ベクトルをその元が同一視される必要はないという性質のものである。20世紀に入ると、数学者たちは新たな対象を扱うようになり、特に数列の空間（級数論も含む）や関数の空間^[7] は自然に線型空間と看做すことができる。実際に、関数の場合なら、関数同士の和や定数をスカラーとする乗法が定義できて、それらの演算は空間ベクトルの加法とスカラー倍が従うのと同じ代数法則に従う。

20世紀の最初の10年間で、ヒルベルト空間の導入に繋がる展開が同時並行的に現れた。その一つは、ヒルベルトとシュミットの積分方程式論の研究過程で見出された^[8]。区間 [a, b] 上の2つの自乗可積分な実数値関数 f, g は「内積」

⟨f,g⟩=∫abf(x)g(x)dx{displaystyle langle f,grangle =int _{a}^{b}f(x)g(x),dx}

を持ち、これがよく知られたユークリッド空間のドット積の性質の多くを有していた。これにより特に、関数からなる正規直交系の概念が意味を持つようになる。シュミットは、この内積と通常のドット積との類似性として、

f(x)↦∫abK(x,y)f(y)dy{displaystyle f(x)mapsto int _{a}^{b}K(x,y)f(y),dy}

（ただし、K は x, y に関して対称）なる形の作用素に対してスペクトル分解の類似物を示した。得られる固有関数展開は関数 K を

K(x,y)=∑nλnφn(x)φn(y){displaystyle K(x,y)=sum _{n}lambda _{n}varphi _{n}(x)varphi _{n}(y),}

なる形の級数として表す。ただし、関数系 φ_n は、n ≠ m なるとき常に ⟨φ_n, φ_m⟩ = 0 を満たすという意味で、直交系を成す。この級数の個々の項は、基本積解 (elementary product solution) と呼ばれることもある。しかし、この固有関数展開には、適当な意味で自乗可積分関数に収束するものとそうでないものがある。収束を保証するには完備性（系の完全性）が不可欠なのである^[9]。

いま一つは、ルベーグがリーマン積分に替わるものとして1904年に導入したルベーグ積分である^[10]。ルベーグ積分は、より広範なクラスの関数で積分を定義することを可能にした。1907年に、リースとフィッシャー（英語版）はそれぞれ独立にルベーグ自乗可積分関数全体の成す空間 L² が完備距離空間であることを示した^[11]。このような幾何学的議論と系の完全性の議論が合わさった帰結として、19世紀に得られたフーリエ、ベッセル、パーシヴァル（英語版）らの三角級数についての成果を、これらのより一般の空間へ容易に持ち込むことができた。そうして得られた幾何学的かつ解析学的な仕組みは今日ではふつうリース・フィッシャーの定理として知られる^[12]。

更なる基本的結果が20世紀の初め頃に証明されていく。例えば、リースの表現定理は1907年にフレシェとリースがそれぞれ独立に示した^[13]フォン・ノイマンは自身の非有界エルミート作用素の研究において「抽象ヒルベルト空間」という用語を創出した^[14]。他のワイルやウィーナーのような数学者は（しばしば物理学的な興味を動機として）既に特定のヒルベルト空間については極めて詳細な研究を行っていたのだけれども、一般のヒルベルト空間をきちんと、しかも公理的に取り扱ったのはフォン・ノイマンが最初である^[15]。後にフォン・ノイマンは、量子力学の基礎付けに関する金字塔的研究^[16]においてこのヒルベルト空間の概念を用いており、ウィグナーへと続いていく。「ヒルベルト空間」という呼称は瞬く間に他へ広まり、例えばワイルは自身の量子力学と群論の教科書^[17]で用いている。

ヒルベルト空間の概念の重要性は、それが最も適切な量子力学の数学的基礎の提供を実現したことで強く認識されるようになった^[18]。簡単に言えば、量子力学系の状態はある種のヒルベルト空間におけるベクトルであり、可観測量はその空間上のエルミート作用素であり、系の対称性はユニタリ作用素であり、観測は直交射影である。量子力学的対称性とユニタリ作用素との間の関係は、1928年のワイル^[17]に始まる群のユニタリ表現論の発展の原動力となった。他方、1930年代の初め頃には、古典的な力学系のある種の性質が、エルゴード理論の枠組みのもとでヒルベルト空間を用いた方法で調べられるようになり、明らかにされた^[19]。

量子力学における可観測量の代数は、ハイゼンベルクの行列力学による量子論の定式化に従って、自然に或るヒルベルト空間上で定義される作用素環となる。1930年代のうちにフォン・ノイマンがヒルベルト空間上の作用素の成す環としての作用素環を調べ始め、フォン・ノイマンやその時代の人々が研究した種類の作用素環は、今日ではフォン・ノイマン環と呼ばれている。1940年代には、ゲルファント、ナイマーク（英語版）、シーガル（英語版）らが C^∗-環と呼ばれる種類の作用素環の定義を与えた。これはヒルベルト空間の基盤となることはない一方で、それまで知られていた作用素環のもつ有用な特徴が当てはまる。特に、存在する殆どのヒルベルト空間論の根底にある、自己随伴作用素のスペクトル定理が C^∗-環に対して一般化された。これらの手法は今や抽象調和解析や表現論において基本となっている。

例

ルベーグ空間

ルベーグ空間は測度空間 (X, M, μ) （X は集合で、M は X の部分集合からなる完全加法族、μ は M 上の完全加法的測度）に付随する関数空間である。L²(X, μ) を、X 上の複素数値可測関数で、その絶対値の平方のルベーグ積分が有限となるようなもの全体の成す空間とする。即ち、L²(X, μ) に属する関数 f は必ず

∫X|f|2dμ<∞{displaystyle int _{X}|f|^{2}dmu <infty }

を満たす。ただし、測度零の集合の上でだけ異なる（殆ど至る所一致する）ような関数は全て同一視するものとする。

L²(X, μ) に属する関数 f, g の内積は

⟨f,g⟩=∫Xf(t)g(t)¯ dμ(t){displaystyle langle f,grangle =int _{X}f(t){overline {g(t)}} dmu (t)}

で与えられる。L² の元 f, g に対して、右辺の積分が存在することはコーシー・シュヴァルツの不等式から示されるから、これは確かに内積を定義している。このように定義された内積に関して L² は実は完備になる^[20]。積分がルベーグ積分であることは完備性を保証するために本質的である。例えば、実数からなる領域上でリーマン可積分関数を考えるのでは十分でない^[21]。

多くの自然な設定の下でルベーグ空間を考えることができる。L²(R) および L²([0, 1]) をそれぞれ実数直線および単位閉区間上で定義される（ルベーグ測度に関する）自乗可積分関数全体の成す空間とすると、それぞれの自然な定義域上でフーリエ変換とフーリエ級数が定義できる。別な状況では、実数直線上の通常のルベーグ測度ではない何か別の測度を用いることもある。例えば、任意の正値可測関数 w をとり、区間 [0, 1] 上の可測関数 f で

∫01|f(t)|2w(t)dt<∞{displaystyle int _{0}^{1}|f(t)|^{2}w(t),dt<infty }

を満たすもの全体の成す空間は重み付き L²-空間と呼ばれ、w を重み関数と呼ぶ。内積は

⟨f,g⟩=∫01f(t)g(t)¯w(t)dt{displaystyle langle f,grangle =int _{0}^{1}f(t){overline {g(t)}}w(t),dt}

で与えられる。重み付き空間 L2
w([0, 1]) はヒルベルト空間 L²([0, 1], μ) に等しい。ただし測度 μ は可測集合 A に対して

μ(A)=∫Aw(t)dt{displaystyle mu (A)=int _{A}w(t),dt}

を満たすものと定める。このような重み付き L² 空間は直交多項式を調べるのによく用いられる（これは種々の直交多項式系は、それぞれ別な重み関数に関する意味で直交することによる）。

ソボレフ空間

ソボレフ空間 H^s あるいは W^s,2 はヒルベルト空間になる。これらの空間は微分が行えるような関数空間の一種で、（ヘルダー空間のようなほかのバナッハ空間とは異なり）内積の構造も持つ特別な場合になっている。微分が使えることで、ソボレフ空間は偏微分方程式論に対して都合がよい^[22]。また変分法における直接法の基礎も与えている。^[23]

非負整数 s と領域 Ω ⊂ Rⁿ に対し、ソボレフ空間 H^s(Ω) は s 階までの弱微分が全て L² に属するような L²-関数を全て含む。H^s(Ω) における内積は

⟨f,g⟩=∫Ωf(x)g¯(x)dx+∫ΩDf⋅Dg¯(x)dx+⋯+∫ΩDsf(x)⋅Dsg¯(x)dx{displaystyle langle f,grangle =int _{Omega }f(x){bar {g}}(x),dx+int _{Omega }Dfcdot D{bar {g}}(x),dx+cdots +int _{Omega }D^{s}f(x)cdot D^{s}{bar {g}}(x),dx}

で与えられる。ただし、右辺のドット積は各階の偏導関数全体の成すユークリッド空間におけるドット積である。s が整数でない場合にもソボレフ空間は定義できる。

ソボレフ空間は、（ヒルベルト空間のより具体的な構造に依拠する）スペクトル論の観点からも研究される。適当な領域 Ω に対してソボレフ空間 H^s(Ω) をベッセルポテンシャル（英語版）全体の成す空間として定義することができる^[24]。これはだいたい

Hs(Ω)={(1−Δ)−s/2f|f∈L2(Ω)}{displaystyle H^{s}(Omega )={(1-Delta )^{-s/2}f|fin L^{2}(Omega )}}

のようなものである。ここで Δ はラプラス作用素、(1 − Δ)^−s/2 はスペクトル写像定理（英語版）によって捉えることができる。非負整数 s に対するソボレフ空間の意味のある定義を与える必要があることをひとまず置いておけば、ソボレフ空間の定義はフーリエ変換のもとで特に望ましい性質を持ち、擬微分作用素の研究に対して理想的である。これらの方法をコンパクトリーマン多様体上で用いれば、例えばホッジ理論の基礎を成すホッジ分解が得られる^[25]。

正則関数の空間

ハーディ空間

複素解析や調和解析で用いられるハーディ空間は、その元が複素領域上の正則関数となっているような関数空間の一種である^[26]。U をガウス平面上の単位円板とすると、ハーディ空間 H²(U) は U 上の正則関数 f で、その平均

Mr(f)=12π∫02π|f(reiθ)|2dθ{displaystyle M_{r}(f)={frac {1}{2pi }}int _{0}^{2pi }|f(re^{itheta })|^{2},dtheta }

がまた r < 1 で抑えられるようなもの全体の成す空間として定義される。このハーディ空間上のノルムは

‖f‖2=limr→1Mr(f){displaystyle |f|_{2}=lim _{rto 1}{sqrt {M_{r}(f)}}}

で与えられる。この円板上のハーディ空間はフーリエ級数と関係があり、正則関数 f が H²(U) に属するための必要十分条件は、

f(z)=∑n=0∞anzn,(∑n=0∞|an|2<∞){displaystyle f(z)=sum _{n=0}^{infty }a_{n}z^{n},qquad left(sum _{n=0}^{infty }|a_{n}|^{2}<infty right)}

なる形に書けることである。従って、空間 H²(U) は、単位円板上の L²-関数で、負の周波数に対するフーリエ係数が消えているようなもの全体からなる。

ベルグマン空間

正則関数の成すヒルベルト空間の別なクラスにベルグマン空間がある^[27]。D をガウス平面（または高次元の複素空間）の有界開集合とし、L^2,h(D) を D 上の正則関数 f で

‖f‖2=∫D|f(z)|2dμ(z)<∞{displaystyle |f|^{2}=int _{D}|f(z)|^{2},dmu (z)<infty }

なる意味で L²(D) にも属するようなもの全体の成す集合とする。ただし積分は D におけるルベーグ測度に関してとる。明らかに L^2,h(D) は L²(D) の部分空間であり、実は閉部分空間になっているので、それ自身ヒルベルト空間を成す。このことは、D のコンパクト部分集合 K の上で有効な評価

supz∈K|f(z)|≤CK‖f‖2{displaystyle sup _{zin K}|f(z)|leq C_{K}|f|_{2}}

からの帰結である。この評価自体はコーシーの積分公式から出る。従って、L²(D) に属する正則関数列の収束はコンパクト収束でもあるから、極限関数もまた正則になる。先の評価不等式の別な帰結として、D の一点において関数 f を評価する線型汎関数は、実際には L^2,h(D) 上で連続であることがわかる。リースの表現定理によれば、この評価関数を表現する L^2,h(D) の元が存在するから、各 z ∈ D に対して関数 η_z ∈ L^2,h(D) で

f(z)=∫Df(ζ)ηz(ζ)¯dμ(ζ){displaystyle f(z)=int _{D}f(zeta ){overline {eta _{z}(zeta )}},dmu (zeta )}

をすべての ƒ ∈ L^2,h(D) に対して満たすようなものが取れる。被積分関数の因子

K(ζ,z)=ηz(ζ)¯{displaystyle K(zeta ,z)={overline {eta _{z}(zeta )}}}

は D のベルグマン核と呼ばれる積分核で、再生性

f(z)=∫Df(ζ)K(ζ,z)dμ(ζ){displaystyle f(z)=int _{D}f(zeta )K(zeta ,z),dmu (zeta )}

を満足する。

ベルグマン空間は再生核ヒルベルト空間（英語版）（関数からなるヒルベルト空間で、先と同様の再生性を持つ積分核 K(ζ,z) を備えたもの）の例になっている。ハーディ空間 H²(D) にもセゲー核（英語版）と呼ばれる再生核を持つ^[28]。再生核は数学のほかの分野でもよく用いられる。たとえば、調和解析におけるポアソン核は単位球体上の自乗可積分調和関数全体の成すヒルベルト空間（これがヒルベルト空間を成すことは調和関数に対する中間値の定理からわかる）に対する再生核である。

応用

ヒルベルト空間の応用の多くは、ヒルベルト空間において射影や基底変換といったような単純な幾何学的概念が、ふつうの有限次元の場合に考えられるそれらの自然な一般化になっているという事実に依拠して行われている。特に、ヒルベルト空間上の連続自己随伴線型作用素のスペクトル論は、行列のふつうのスペクトル分解の一般化であり、これはヒルベルト空間論を他の数学や物理学の分野に応用する際にしばしば大きな役割を果たす。

スツルム・リウヴィル理論

振動元の倍音。これらはスツルム・リウヴィル問題の固有関数で、固有値 1,1/2,1/3,… は倍音列を成す。

常微分方程式論において、微分方程式の固有関数および固有値の振る舞いを調べるのに適当なヒルベルト空間上のスペクトル法が利用できる。例えば、ヴァイオリンの弦やドラムの調波の研究から生じたスツルム・リウヴィル問題は、常微分方程式論の中心的な問題である^[29]。スツルム・リウヴィル問題は区間 [a, b] 上の未知関数 y に対する常微分方程式

−ddx[p(x)dydx]+q(x)y=λw(x)y{displaystyle -{frac {d}{dx}}left[p(x){frac {dy}{dx}}right]+q(x)y=lambda w(x)y}

で、一般斉次ロビン境界条件

{αy(a)+α′y′(a)=0βy(b)+β′y′(b)=0.{displaystyle {begin{cases}alpha y(a)+alpha 'y'(a)=0\beta y(b)+beta 'y'(b)=0.end{cases}}}

を満足するものである。関数 p, q, および w は所与で、方程式の解となる関数 y および定数 λ を求める。同問題は、この系の固有値と呼ばれる特定の値の λ に対してだけ解を持つのだが、それのことはこの系に対するグリーン関数によって定まる積分作用素にコンパクト作用素のスペクトル論を適用した結果として得られる。さらにはこの一般論からの別な帰結として、固有値 λ を無限大に発散する単調増大列に並べることができる^[30]。

偏微分方程式論

ヒルベルト空間は偏微分方程式を調べる基本的な道具である^[22]。即ち、楕円型線型方程式のような偏微分方程式の多くのクラスでは、考える関数のクラスを拡張して弱解と呼ばれる超関数解を考えることができるが、弱解の定式化（弱定式化）の多くはヒルベルト空間を成すソボレフ関数のクラスを含むものになっているのである。解を求めたり、あるいはしばしばより重要な、与えられた境界条件に対する解の存在および一意性を示したりする解析学的な問題が、適当な弱定式化によって幾何学的問題に還元される。楕円型線型方程式に対して、かなりのクラスの問題が一意的に解けることを保証する幾何学的結果の一つがラックス・ミルグラムの定理（英語版）である。この方法論は、偏微分方程式の数値解法に対するガレルキン法（英語版）（有限要素法の一つ）の基盤をなしている^[31]。

典型的な例が、R² の有界領域 Ω におけるポアソン方程式 −Δu = g のディリクレ境界問題である。弱定式化は、境界上で消えている Ω 上連続的微分可能な任意の関数 v に対して

∫Ω∇u⋅∇v=∫Ωgv{displaystyle int _{Omega }nabla ucdot nabla v=int _{Omega }gv}

を満たすような関数 u を求めることからなる。これは、u およびその弱偏導関数がともに境界上で消えている Ω 上の自乗可積分関数となるような関数 u からなるヒルベルト空間 H1
0(Ω) の言葉で書き直すことができて、問題はこの空間 H1
0(Ω) の任意の元 v に対して

a(u,v)=b(v){displaystyle a(u,v)=b(v)}

を満たすような u を空間 H1
0(Ω) の中で求めることに帰着される。ただし、a および b はそれぞれ

a(u,v)=∫Ω∇u⋅∇v,b(v)=∫Ωgv{displaystyle a(u,v)=int _{Omega }nabla ucdot nabla v,quad b(v)=int _{Omega }gv}

で与えられる連続な双線型形式および連続な線型汎関数である。ポアソン方程式は楕円型だから、ポアンカレの不等式から双線型形式 a が強圧的（英語版）であることが従う。故に、ラックス・ミルグラムの定理は、この方程式の解の存在と一意性を保証する。

多くの楕円型偏微分方程式に対して同様のやり方でヒルベルト空間による定式化ができるので、それ故にラックス・ミルグラムの定理はそれらの解析における基本的な道具となる。同様の方法は抛物型偏微分方程式やある種の双曲型偏微分方程式に対しても、適当な修正を施せば通用する。

エルゴード理論

ブニモヴィチスタジアムにおける力学的ビリヤード球の軌道は、エルゴード力学系で記述される。

エルゴード理論の分野では、カオス力学系の長期的振る舞いを研究する。エルゴード理論が有効な原型的な場合というのは、熱力学における系である。この系の微視的な状態は（微粒子の間の個々の衝突の集まりとしては理解できないという意味で）極めて複雑であるにも拘らず、十分長期間にわたるその平均的振る舞いは素直であり、熱力学の法則が主張するのはこのような平均的挙動である。特に、熱力学の第0法則は「十分長い時間スケールを経れば平衡状態にある熱力学系の、その機能的に独立な測度は、温度の形でのその全エネルギーのみである」などと定式化できる。

エルゴート力学系は、（ハミルトニアンで測られる）エネルギーを除けば、相空間上の機能的に独立な保存量を持たないような系である。詳しく述べれば、エネルギー E を固定して、Ω_E をエネルギーが E となる状態すべてからなる相空間の部分集合（エネルギー面）とし、T_t で相空間上の発展演算子を表せば、力学系がエルゴードとなるのは、Ω_E 上の定数でない連続関数で、Ω_E の任意の w と任意の時間 t において

f(Ttw)=f(w){displaystyle f(T_{t}w)=f(w)}

を満たすものがない場合に限る。リウヴィルの定理によれば、エネルギー面上の測度 μ で時間並進不変なものが存在する。結果として時間並進は、エネルギー面 Ω_E 上の自乗可積分関数に内積を

⟨f,g⟩L2(ΩE,μ)=∫Efg¯dμ{displaystyle langle f,grangle _{L^{2}(Omega _{E},mu )}=int _{E}f{bar {g}},dmu }

で入れたヒルベルト空間 L²(Ω_E,μ) のユニタリ変換になる。

フォンノイマンの平均エルゴード定理^[19]の主張は次のようなものである。

• 
  U_t がヒルベルト空間 H 上のユニタリ作用素からなる（強連続）一径数半群で、P を U_t の同時不動点全体の成す集合{x∈H | U_tx = x for all t > 0} の上への直交射影とすると
  Px=limT→∞1T∫0TUtxdt{displaystyle Px=lim _{Tto infty }{frac {1}{T}}int _{0}^{T}U_{t}x,dt}
  が成り立つ。

エルゴード系では、時間発展の固定集合は定数関数のみから成るので、先のエルゴード定理から任意の f ∈ L²(Ω_E,μ) に対し

L2-limT→∞1T∫0Tf(Ttw)dt=∫ΩEf(y)dμ(y){displaystyle {underset {Tto infty }{L^{2}!{text{-}}!lim {}}}{frac {1}{T}}int _{0}^{T}f(T_{t}w),dt=int _{Omega _{E}}f(y),dmu (y)}

となることが従う^[32]。つまり、観測可能な f の長期平均は、そのエネルギー面に亘ってとった期待値に等しい。

フーリエ解析

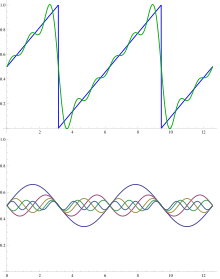
正弦波基底関数（下）の重ね合わせが鋸歯状波（上）になる。

球面上の自乗可積分関数全体の成すヒルベルト空間の正規直交基底を成す球面調和関数を、半径方向に沿ってグラフ化したもの

フーリエ解析の基本目的の一つは、関数を付随するフーリエ級数、即ち与えられた基底関数族の（必ずしも有限とは限らない）線型結合に分解することである。区間 [0, 1] 上の関数 f に付随する古典フーリエ級数とは

∑n=−∞∞ane2πinθ(an:=∫01f(θ)e−2πinθdθ){displaystyle sum _{n=-infty }^{infty }a_{n}e^{2pi intheta }quad (a_{n}:=int _{0}^{1}f(theta )e^{-2pi intheta },dtheta )}

なる形の級数である。

鋸歯状波関数に対するフーリエ級数の最初の数項を足し上げた例を図に示す。鋸歯状波関数の波長を λ とすると、（基本波、つまり n = 1 を除いて）それよりも短い波長 λ/n（n は整数）をもつ正弦波が基底関数である。全ての基底関数が鋸歯状波の折れるところで交わり（結点）を持つが、基本波を除く全ての基底関数はそれ以外にも結点を持つ。鋸歯の周りでの基底関数の部分和の振動はギブズ現象と呼ばれるものである。

古典フーリエ級数論の特徴的な問題の一つに「関数 f のフーリエ級数がもとの関数に収束する（ことが仮にあったとする）ならば、それはどのような意味においての収束であるか」を問う問題がある。これに対して、ヒルベルト空間を用いた方法で答えを与えることができる^[33]。関数族 e_n(θ) := e^2πinθ はヒルベルト空間 L²([0, 1]) の正規直交基底を成すから、それ故に任意の自乗可積分関数 f が

f(θ)=∑nanen(θ),(an:=⟨f,en⟩){displaystyle f(theta )=sum _{n}a_{n}e_{n}(theta ),quad (a_{n}:=langle f,e_{n}rangle )}

なる級数の形で表せて、さらにこの級数は L²([0, 1]) の元として収束する（即ち、L²-収束、自乗平均収束）。

この問題を抽象的な観点からも見ることができる。任意のヒルベルト空間は正規直交基底を持ち、ヒルベルト空間の各元はそれら基底に属する元の定数倍の和として一意的に表すことができるが、この展開に現れる各基底元の係数のことをその元の抽象フーリエ係数と呼ぶことがある^[34]。このような抽象化は、L²([0,1]) などの空間で別の基底関数系を用いることがより自然であるようなときに、特に有用である。関数を三角関数系に分解することは不適当だが、例えば直交多項式系やウェーブレット^[35]および高次元において球面調和関数^[36]へ展開することが適当であるような状況はたくさんある。

例えば、e_n を L²[0,1] の任意の正規直交基底関数系とすると、与えられた L²[0,1] の関数は有限線型結合

f(x)≈fn(x)=a1e1(x)+a2e2(x)+⋯+anen(x){displaystyle f(x)approx f_{n}(x)=a_{1}e_{1}(x)+a_{2}e_{2}(x)+cdots +a_{n}e_{n}(x)}

で近似することができる^[37]。右辺の係数 {a_j} は、差の大きさ ‖ƒ − ƒ_n‖² をできるだけ小さくするように定める。幾何学的には、最適近似は {e_j} の線型結合全体の成す部分空間の上への ƒ の直交射影であり、

aj=∫01ej(x)¯f(x)dx{displaystyle a_{j}=int _{0}^{1}{overline {e_{j}(x)}}f(x),dx}

によって計算することができる^[38]。これが ‖ƒ − ƒ_n‖² を最小化することはベッセルの不等式とパーセヴァルの公式からの帰結である。

種々の物理学的問題においては、関数を物理的に意味を持つ微分作用素（典型的なものはラプラス作用素）の固有関数系に分解することができ、微分作用素のスペクトルに関連して、関数のスペクトル研究の基礎を成している^[39]。物理学への具体的な応用として太鼓の形を聴く（英語版）問題が挙げられる。これは「太鼓の皮が引き起こす基本振動モードを与えたとき、太鼓自身の形が推定できるか」というものである^[40]。この問題の数学的定式化は、平面上のラプラス作用素のディリクレ固有値に関わるものになる（これはヴァイオリンの弦の基本振動モードを表す整数の直接の対応物である）。

スペクトル論も関数のフーリエ変換のある種の側面を下支えしている。フーリエ解析ではコンパクト集合上定義された関数を（ヴァイオリンの弦や太鼓の皮の振動に対応する）ラプラス変換の離散スペクトルに分解するのに対して、関数のフーリエ変換はユークリド空間の全域で定義された関数をラプラス作用素の連続スペクトル（英語版）に関する成分に分解する。フーリエ変換があるヒルベルト空間（「時間領域」）から別なヒルベルト空間（「周波数領域」）への等距変換であることを主張するプランシュレルの定理として、フーリエ変換は幾何学的な意味を持つ。このフーリエ変換の等距性は、例えば非可換調和解析に現れる球関数に対するプランシュレルの定理などが示すとおり、抽象的な調和解析では繰り返し登場する主題である。

量子力学

水素原子における電子の軌道はエネルギーの固有関数である。

ディラック^[41]とフォンノイマン^[42]によって発展した量子力学の数学的に厳密な定式化は、量子力学系の取りうる状態（より正確には純粋状態）が、状態空間と呼ばれる可分な複素ヒルベルト空間に属する単位ベクトル（状態ベクトルという）によって（位相因子と呼ばれるノルム 1 の複素数の違いを除いて）表現される。つまり、取りうる状態はあるヒルベルト空間の射影化（ふつうは複素射影空間と呼ばれる）の元である。このヒルベルト空間が実際にどのようなものになるかは系に依存する。例えば、一つの非相対論的スピン 0 粒子の位置と運動量の状態は自乗可積分関数全体の成す空間であり、いっぽう一つの陽子のスピンの状態はスピノルの成す二次元複素ヒルベルト空間の長さ 1 の元である。各可観測量は状態空間上に作用する自己随伴線型作用素として表現され、可観測量の固有状態はその作用素の固有ベクトルに、固有ベクトルに対応する固有値は固有状態にある可観測量の値にそれぞれ対応する。

量子状態の時間発展はシュレーディンガー方程式によって記述され、そこに現れるハミルトニアン（全エネルギーに対応する作用素）は時間発展を生み出す。

二つの状態ベクトルの間の内積は確率振幅として知られる複素数になる。量子力学系の理想的な測定の間で、系が与えられた初期状態から特定の固有状態に崩壊する確率は、初期状態から終期状態の間の確率振幅の絶対値の平方によって与えられる。測定の結果として可能なのは、作用素の固有値であり（これは自己随伴作用素のとり方を説明する）、全ての固有値は実数でなければならない。与えられた状態の可観測量の確率分布は対応する作用素のスペクトル分解を計算すれば求められる。

一般の系では、状態は典型的には純粋ではないが、密度行列（ヒルベルト空間上のトレース 1 の自己随伴作用素）で与えられる純粋状態の統計的混合（あるいは混合状態）として表される。さらに、一般の量子力学系では、単独の測定の効果は系のほかの部分に影響を及ぼしうるが、それは測度が正の作用素値測度（英語版）で取り替えたものとして記述される。従って、一般論として状態と可観測量の両方の構造は、純粋状態の理想化したものより相当に複雑である。

ハイゼンベルクの不確定性原理は、ある種の可観測量に対応する作用素が互いに可換でなく、特定の形の交換子を与えるという主張として表される。

性質

三平方の定理

ヒルベルト空間 H の二つのベクトル u, v が直交するのは、〈u, v〉 = 0 のときである。このとき u ⊥ v と書く。更に一般に、H の部分集合 S に対して u ⊥ S と書けば、これは u が S の各元と直交することを意味する。

u と v とが直交するとき、等式

‖u+v‖2=⟨u+v,u+v⟩=⟨u,u⟩+2Re⟨u,v⟩+⟨v,v⟩=‖u‖2+‖v‖2{displaystyle |u+v|^{2}=langle u+v,u+vrangle =langle u,urangle +2,mathrm {Re} langle u,vrangle +langle v,vrangle =|u|^{2}+|v|^{2}}

が成り立つ。これは個数 n に関する帰納法で拡張することができて、任意の互いに直交する n 本のベクトルの族
u₁, …, u_n に対して

‖u1+⋯+un‖2=‖u1‖2+⋯+‖un‖2{displaystyle |u_{1}+cdots +u_{n}|^{2}=|u_{1}|^{2}+cdots +|u_{n}|^{2}}

が成り立つ。三平方の定理の主張は任意の内積空間で有効であるにも拘らず、この等式を級数（無限和）に対して拡張するには完備性を課さねばならない。互いに直交するベクトルからなる級数 ∑ u_k が H において収束するための必要十分条件は、各項のノルムの平方からなる級数が収束し、かつ

‖∑k=0∞uk‖2=∑k=0∞‖uk‖2{displaystyle left|sum _{k=0}^{infty }u_{k}right|^{2}=sum _{k=0}^{infty }|u_{k}|^{2}}

が満たされることである。更に言えば、互いに直交するベクトルからなる級数の和は、それらのベクトルの和をとる順番に依らずに定まる。

中線定理と極化公式

幾何学的には、中線定理の式は AC² + BD² = 2(AB² + AD²) なることを示すものである。言葉で書けば、対角線の平方和は任意の隣り合う二辺の平方和の二倍に等しい。

定義から、任意のヒルベルト空間はバナッハ空間であり、さらに中線定理

‖u+v‖2+‖u−v‖2=2(‖u‖2+‖v‖2){displaystyle |u+v|^{2}+|u-v|^{2}=2(|u|^{2}+|v|^{2})}

も成立する。逆に中線定理が成り立つような任意のバナッハ空間はヒルベルト空間になり、その内積は極化恒等式（英語版）によってノルムから一意的に定まる^[43]。実ヒルベルト空間における極化恒等式は

⟨u,v⟩=14(‖u+v‖2−‖u−v‖2){displaystyle langle u,vrangle ={frac {1}{4}}(|u+v|^{2}-|u-v|^{2})}

であり、複素ヒルベルト空間の場合は

⟨u,v⟩=14(‖u+v‖2−‖u−v‖2+i‖u+iv‖2−i‖u−iv‖2){displaystyle langle u,vrangle ={frac {1}{4}}(|u+v|^{2}-|u-v|^{2}+i|u+iv|^{2}-i|u-iv|^{2})}

で与えられる。中線定理は、任意のヒルベルト空間が一様凸バナッハ空間（英語版）となることを示している^[44]。

最適近似

ヒルベルト空間 H の空でない閉凸部分集合を C とし、H の点 x をとると、x との距離を最小化する C の元 y がただ一つ存在する^[45]。

∃!y∈C,‖x−y‖=dist(x,C)=min{‖x−z‖:z∈C}.{displaystyle {}^{exists !}yin C,quad |x-y|=mathrm {dist} (x,C)=min{|x-z|:zin C}.}

これは、C を平行移動した凸集合 D := C − x にノルムが最小となる点が存在するとも言い換えられる。このことは、任意の最小化列 (d_n) ⊂ D が（中線定理により）コーシー列となること、従って（完備性により）D 内の点に収束するが、それがノルム最小であることを示すことで証明できる。もっと一般に、一様凸バナッハ空間でこのことは成り立つ^[46]。

この結果を H の閉部分空間 F に適用するとき、y ∈ F が x に最近接することは

y∈F,x−y⊥F{displaystyle yin F,quad x-yperp F}

によって特徴付けることができる^[47]。この点 y というのは x の F の上への直交射影に他ならない。このとき、写像 P_F: x ↦ y は線型である（後述）。この結果は、最小自乗法の基礎を成すもので、応用数学、特に数値解析において有意である。

特に F が全体空間 H 自身とは一致しないとき、F に直交する非零ベクトル v が取れる（F に属さない x をとって、v := x − y と置けばよい）。これを応用して、閉部分集合 F が H の部分集合 S によって生成されるかを見るのに有効な判定法が得られる。即ち、

H の部分集合 S が生成する部分空間が H で稠密となるのは、S に直交するベクトル v ∈ H が零ベクトル 0 のみであるとき（かつそのときに限る）である。

双対性

ヒルベルト空間 H の連続的双対空間 H^∗ とは、H からその係数体への連続な線型写像全体の成す空間のことをいう。この空間には

‖φ‖=sup‖x‖=1,x∈H|φ(x)|{displaystyle |varphi |=sup _{|x|=1, atop xin H}|varphi (x)|}

で定義される自然なノルムが入る。このノルムは中線定理を満足するので、この双対空間もまた内積空間になる。またこれは完備であり、従ってそれ自身ヒルベルト空間を定める。

リースの表現定理は、この双対空間の簡便な記述を与えてくれる。即ち、H の各元 u に対して、

φu(x)=⟨x,u⟩{displaystyle varphi _{u}(x)=langle x,urangle }

で定まる H^∗ の元 φ_u がただ一つ存在し、写像 u ↦ φ_u は H から H^∗ への反線型写像（英語版）になる。リースの表現定理はこの写像が反線型同型であるというのである^[48]。故に、双対空間 H^∗ の各元 φ に対し H の元 u_φ がただ一つ存在して、H の任意の元 x について

⟨x,uφ⟩=φ(x){displaystyle langle x,u_{varphi }rangle =varphi (x)}

を満たす。双対空間 H^∗ 上に定まるこの内積は

⟨φ,ψ⟩=⟨uψ,uφ⟩{displaystyle langle varphi ,psi rangle =langle u_{psi },u_{varphi }rangle }

を満たす。右辺で順番が逆になっているのは u_φ の反線型性から φ の線型性を回復するためである。実係数の場合は、H からその双対空間への反線型同型は実際には線型同型になるから、実ヒルベルト空間はその双対空間と自然に同型になる。

表現ベクトル u_φ を得るには以下のようにする。φ ≠ 0 のとき、核 F = ker φ は H の閉部分空間であって、H には一致しないから、F に直交する非零ベクトル v が存在する。ベクトル u を v の適当なスカラー倍 λv として、φ(v) = 〈v, u〉 が

u=⟨v,v⟩−1φ(v)¯v{displaystyle u=langle v,vrangle ^{-1},{overline {varphi (v)}},v}

を満たすようにする。この対応関係 φ ↔ u は物理学ではお馴染みのブラ・ケット記法で大いに活用されている。物理学ではふつうは内積 〈x | y〉 の右側の項に関して線型なので、

⟨x∣y⟩:=⟨y,x⟩{displaystyle langle xmid yrangle :=langle y,xrangle }

とすると、この 〈x | y〉 は、ブラベクトルと呼ばれる線型汎関数 〈x| がケットベクトルと呼ばれるベクトル |y〉 に作用したものと見ることができる。

リースの表現定理は内積の存在に関して基本的であるばかりでなく、双対空間の完備性に関しても基本的である。事実、定理からは任意の内積空間の位相的双対がもとの空間の完備化と同一視できることが導かれる。リースの表現定理から直ちに導かれる結果としては他にも、ヒルベルト空間 H の回帰性、即ち H からその二重双対空間への自然な写像が同型となることも挙げられる。

弱収束列

ヒルベルト空間 H において、点列 {x_n} がベクトル x ∈ H に弱収束するとは、任意の v ∈ H に対し

limn⟨xn,v⟩=⟨x,v⟩{displaystyle lim _{n}langle x_{n},vrangle =langle x,vrangle }

をみたすことをいう。

例えば、任意の正規直交列 {ƒ_n} は 0 に弱収束することが、ベッセルの不等式から従う。任意の弱収束列 {x_n} は一様有界性原理（英語版）により有界である。

逆に、ヒルベルト空間における任意の有界列は弱収束する部分列を含む（アラオグルの定理） ^[49]。この結果は、R^d 上の連続関数に対してボルツァーノ・ヴァイエルシュトラスの定理を用いるのと同じやり方で、連続凸関数に対する最小値定理の証明に用いられる。これにはいくらか異なった述べ方があるが、以下のような形が簡便であろう^[50]

ƒ: H → R が凸関数で、‖x‖ → ∞ のとき ƒ(x) → +∞ を満たすとき、ƒ は H の適当な点 x₀ ∈ H で最小値を持つ。

この事実（とその種々の一般化）は変分法における直接法の基礎を成している。有界閉凸関数に対する最小値の存在は、もう少し抽象的な、ヒルベルト空間 H 内の有界閉凸部分集合が H の回帰性により弱コンパクトになるという事実からも直接的に得られる。弱収束部分列の存在性は、エーベルライン・スムリアンの定理（英語版）の特別の場合である。

バナッハ空間の性質

バナッハ空間が一般に持つ性質はヒルベルト空間においても成立する。開写像定理の主張は「バナッハ空間からバナッハ空間への連続かつ全射な線型写像は、開集合を開集合に写すという意味で開写像である」ことをいい、その系としての有界逆写像定理は「バナッハ空間からバナッハ空間への連続全単射な線型写像は（逆写像も連続であるような連続線型写像の意味で）同型である」ことを主張する。ヒルベルト空間版のこの定理の証明は、一般のバナッハ空間でやるよりも随分と簡単になる^[51]。開写像定理は閉グラフ定理と同値である。後者は「バナッハ空間からバナッハ空間への線型写像が連続となるための必要十分条件がそのグラフが閉集合となることである」ことを主張するものである^[52]。ヒルベルト空間の場合には、これが非有界作用素の研究において基本になる（閉作用素参照）。

（幾何学的な）ハーン・バナッハの定理は、閉凸集合をその外にある任意の点からヒルベルト空間の超平面によって分割できることを示すものである。これは最適近似性から直ちに得られる。即ち、y が閉凸集合 F の元で x に最近接するものとすると、線分 xy に垂直で、その中点を通る平面が求める分割超平面である^[53]。

ヒルベルト空間上の線型作用素

有界作用素

ヒルベルト空間 H₁ から別のヒルベルト空間 H₂ への連続線型作用素 A: H₁ → H₂ は有界集合を有界集合へ写すという意味で「有界」である。逆に、有界な線型作用素は連続になる。二つの有界線型作用素の和および合成は、ふたたび有界かつ線型であり、このような有界線型作用素全体の成す空間には、作用素ノルムと呼ばれるノルム

‖A‖=sup{‖Ax‖:‖x‖≤1}{displaystyle lVert ArVert =sup{,lVert AxrVert :lVert xrVert leq 1}}

が定義される。また、H₂ の元 y に対して、x ∈ H₁ を 〈Ax, y〉 へ写す写像は線型かつ連続である。リースの表現定理によれば、有界線型作用素は必ず H₁ の適当なベクトル A^∗y に対する

⟨x,A∗y⟩=⟨Ax,y⟩{displaystyle langle x,A^{*}yrangle =langle Ax,yrangle }

の形で表現可能である。この定義から、もう一つの有界線型作用素（A の随伴作用素）A^∗: H₂ → H₁ が定まる。このとき、A^∗∗ = A であることが確かめられる。

H 上の有界線型作用素全体の成す集合 B(H) に、作用素の加法と合成および作用素ノルムと随伴作用素を考えたものは、作用素環の一種である C^∗-環を成す。

B(H) の元 A は A^∗ = A を満たすとき自己随伴作用素もしくはエルミート作用素と呼ばれる。エルミート作用素 A が 〈Ax, x〉 ≥ 0 を任意の x で満たすとき、A は非負であるといい、A ≥ 0; で表す。さらに等号成立が x = 0 のときに限るならば A は正であるという。また、

A − B ≥ 0 ならば A ≥ B

なるものと定義すれば、自己随伴作用素全体の成す集合に半順序 ≥ が導入できる。作用素 A が適当な B に対して A = B^∗B なる形に書けるならば、A は非負であり、さらに B が可逆のとき A は正になる。また、非負作用素 A に対して

A=B2=B∗B{displaystyle A=B^{2}=B^{*}B}

を満たす非負平方根 B が一意に定まるという意味で逆が成り立つ。これは、スペクトル論によって精緻化することができ、自己随伴作用素を「実」作用素と看做すことが有効であると分かる。B(H) の元 A が A^∗A = A A^∗ を満たすとき、A は正規であるという。正規作用素は、自己随伴作用素と自己随伴作用素の虚数倍の和

A=A+A∗2+i(A−A∗)2i{displaystyle A={frac {A+A^{*}}{2}}+i{frac {(A-A^{*})}{2i}}}

に分解され、各項は互いに可換になる。正規作用素をその実部と虚部とに分けて考えることも有用である。

B(H) の元 U が可逆かつその逆作用素が U^∗ で与えられるとき、U はユニタリであるという。この条件は「U が全射かつ H の各元 x, y に対して 〈Ux, Uy〉 = 〈x, y〉 を満たすこと」とも言い換えられる。H 上のユニタリ作用素の全体は、合成に関して H の等距変換群と呼ばれる群を成す。

B(H) の元がコンパクトであるとは、それが有界集合を相対コンパクト集合へ写すときに言う。同じことだが、有界作用素 T について、任意の有界列 {x_k} に対して列 {Tx_k} が収束部分列を持つとき T はコンパクトである。多くの積分作用素はコンパクトであり、事実ヒルベルト＝シュミット作用素として知られるコンパクト作用素のクラスが積分方程式論において特に重要な働きをする。フレドホルム作用素は恒等変換の定数倍の分だけコンパクト作用素とは違うけれども、核と余核が有限であるような作用素としても特徴付けられる。フレドホルム作用素の指数 (index) は

indexT=dim⁡ker⁡T−dim⁡cokerT.{displaystyle operatorname {index} ,T=dim ker T-dim operatorname {coker} ,T.}

で定義される。この指数はホモトピー不変量であり、アティヤ・シンガーの指数定理を通じて微分幾何学で深い役割を果たす。

非有界作用素

ヒルベルト空間においては非有界作用素もある程度きれいに扱うことができ、量子力学にも重要な応用を持つ^[54]。ヒルベルト空間 H 上の非有界作用素 T は、その定義域 D(T) が H の線型部分空間であるような線型作用素であるものとして定義される。定義域が H の稠密な部分集合となることもよくあり、そのような作用素 T は密定義作用素と呼ばれる。

密定義非有界作用素の随伴は、本質的に有界作用素の場合と同じ方法で定義される。自己随伴非有界作用素は量子力学の数学的基礎において可観測量の役割を持つ。ヒルベルト空間 H = L²(R) 上の自己随伴非有界作用素の例としては、

• 微分作用素の適当な拡張
  (Af)(x)=iddxf(x),{displaystyle (Af)(x)=i{frac {d}{dx}}f(x),}
  ただし、i は虚数単位、f は台がコンパクトな可微分関数。


• 
  x による掛け算作用素
  (Bf)(x)=xf(x).{displaystyle (Bf)(x)=xf(x).}
  
  

などが挙げられる^[55]。これらはそれぞれ、運動量と位置の可観測量に対応する。この A も B も H の全域で定義されてはいないことに注意すべきである。A の場合は微分が存在しないものがあること、B の場合は x が掛けられた関数が自乗可積分とは限らないことがその理由である。何れの場合にも、引数にとり得る関数全体の成す集合は H の稠密な部分集合になる。

ヒルベルト空間の構成

直和

二つのヒルベルト空間 H₁ および H₂ を足し併せて、（直交）直和と呼ばれる別のヒルベルト空間 H₁ ⊕ H₂ を作ることができる^[56]。この空間は(x₁, x₂) (x_i ∈ H_i, i = 1,2) なる順序対の全体からなる集合を台に持ち、その上の内積を

⟨(x1,x2),(y1,y2)⟩H1⊕H2:=⟨x1,y1⟩H1+⟨x2,y2⟩H2.{displaystyle langle (x_{1},x_{2}),(y_{1},y_{2})rangle _{H_{1}oplus H_{2}}:=langle x_{1},y_{1}rangle _{H_{1}}+langle x_{2},y_{2}rangle _{H_{2}}.}

で定めたものになっている。より一般に、i ∈ I を添字とするヒルベルト空間の族 H_i に対して、その（外部）直和 ⨁i∈IHi{displaystyle textstyle bigoplus _{iin I}H_{i}} が、H_i のデカルト積の元 x=(xi∈Hi∣i∈I)∈∏i∈IHi{displaystyle textstyle x=(x_{i}in H_{i}mid iin I)in prod _{iin I}H_{i}} で条件 ∑i∈I‖xi‖2<∞{displaystyle textstyle sum _{iin I}|x_{i}|^{2}<infty } を満たすもの全体から成る集合を台とし、内積を

⟨x,y⟩=∑i∈I⟨xi,yi⟩Hi{displaystyle langle x,yrangle =sum _{iin I}langle x_{i},y_{i}rangle _{H_{i}}}

で定めることによって定義される。このとき、各空間 H_i は直和空間の中へ閉部分空間として埋め込まれる。もっと言えば、埋め込まれた各 H_i はどの二つも互いに直交する。逆に、一つのヒルベルト空間において閉部分空間の族 V_i (i ∈ I) で各空間がどの二つも互いに直交しているようなものが与えられているとき、それら全ての和集合が全体空間 H の中で稠密になるならば、H は本質的に V_i たちの直和に同型である。この場合、H は V_i たちの内部直和であると言われる。（内部でも外部でも）直和には、i-番目の直和因子 H_i の上への直交射影 E_i の族が伴う。これらの直交射影はどれも有界・自己随伴かつ冪等な作用素であって、直交性条件

EiEj=0(i≠j){displaystyle E_{i}E_{j}=0quad (ineq j)}

が成り立つ。

ヒルベルト空間 H 上の自己随伴コンパクト作用素に対するスペクトル論によれば、H は或る作用素の固有空間の直交直和に分解され、またその作用素はその固有空間への射影の直和として明示的に表される。ヒルベルト空間の直和は、（素粒子を変数にもつ系のフォック空間など）量子力学においても用いられ、そこでは直和の各成分たるヒルベルト空間と量子力学系の余剰自由度とが対応する。表現論におけるピーター・ワイルの定理（英語版）によれば、ヒルベルト空間上で定義されるコンパクト群のユニタリ表現は必ず有限次元表現の直和に分解されることが保証される。

テンソル積

二つのヒルベルト空間 H₁, H₂ に対し、それらの（代数的な）テンソル積の上に、次のように内積を定めることができる。まず（生成元である）単純テンソル（英語版）に対して

⟨x1⊗x2,y1⊗y2⟩:=⟨x1,y1⟩⟨x2,y2⟩{displaystyle langle x_{1}otimes x_{2},,y_{1}otimes y_{2}rangle :=langle x_{1},y_{1}rangle ,langle x_{2},y_{2}rangle }

と定め、これを半双線型 (Sesquilinearly) に H1⊗H2{displaystyle H_{1}otimes H_{2}} 全体で定義される内積に拡張する。H₁ と H₂ とのヒルベルトテンソル積 H1⊗^H2{displaystyle H_{1}{hat {{}otimes {}}}H_{2}} とは、いま定義した内積に付随する距離位相に関して H₁ ⊗ H₂ を完備化して得られるものをいう^[57]。

ヒルベルト空間 L²([0, 1]) を使って例を考えよう。L²([0, 1]) の二つのコピーのヒルベルトテンソル積は、正方形 [0, 1]² 上の自乗可積分関数の空間 L²([0, 1]²) に等距かつ線型に同型である。この同型で単純テンソル f₁ ⊗ f₂ は

(s,t)↦f1(s)f2(t){displaystyle (s,t)mapsto f_{1}(s),f_{2}(t)}

なる正方形上の関数に写される。

この例は以下のような意味で典型的である^[58]。即ち、各単純テンソル積 x₁ ⊗ x₂ には（連続的）双対 H₁^∗ から H₂ への 1-階作用素

x∗∈H1∗→x∗(x1)x2{displaystyle x^{*}in H_{1}^{*}to x^{*}(x_{1}),x_{2}}

が対応し、この単純テンソル上定義された写像を拡張して、H₁ ⊗ H₂ と H₁^∗ から H₂ への有限階作用素全体の成す空間とを同一視する線型同型が得られる。これを拡張して、ヒルベルトテンソル積 H1⊗^H2{displaystyle H_{1}{hat {{}otimes {}}}H_{2}} は H₁^∗ から H₂ へのヒルベルト＝シュミット作用素全体の成すヒルベルト空間 HS(H₁^∗, H₂) に等距線型同型になることがわかる。

正規直交基底

線型代数学で言うような正規直交基底の概念を、ヒルベルト空間に対するものへ一般化することができる^[59]。ヒルベルト空間 H における正規直交基底とは、H の元からなる族 {e_k}_{k ∈ B} で、条件

1. 
   直交性: B のどの相異なる二元についても、対応する H の元は互いに直交する（⟨e_k, e_j⟩ = 0 for all k, j in B with k ≠ j）。


2. 
   正規性: 族 e_k (k ∈ B) の各元のノルムは 1 である（‖e_k‖ = 1 for all k in B）。


3. 
   完全性: 族 e_k (k ∈ B) の張る部分空間は H において稠密である。

を満足するものを言う。

上記基底の条件の最初の二つを満たすようなベクトルの集合は正規直交系と呼ばれる（B が可算のときは、正規直交列とも呼ぶ）。正規直交系は常に一次独立系である。ヒルベルト空間のベクトルの成す正規直交系については、その完全性条件を次のように言い換えることもできる。

全ての k ∈ B に対して ⟨v, e_k⟩ = 0 を満たす v ∈ H が存在するならば、必ず v = 0 である。

このことは「稠密な部分集合に対して直交するようなベクトルは零ベクトルに限る」という事実と関係がある。実際、S を任意の正規直交系とし、ベクトル v が S に直交するものとすると、v は S の張る部分空間の閉包とも直交するが、S が完全であるならばそのような閉包は全空間に他ならない。

正規直交基底の例としては、

• 集合 {(1,0,0), (0,1,0), (0,0,1)} はドット積に関して R³ の正規直交基底になる。


• 指数関数列 {ƒ_n : n ∈ Z} (ƒ_n(x) = exp(2πinx)) は L²([0, 1]) の正規直交基底になる。

等を挙げることができる。

無限次元の場合には、正規直交基底は線型代数学でいう意味での基底にはならない（これを区別する意味で後者をハメル基底とも呼ぶ）。基底ベクトルの張る部分空間が全空間において稠密であるということから、空間の各ベクトルが基底ベクトルの無限線型和として書けることが従う。また直交性からはそのような和としての表示の一意性が従う。

数列空間の場合

自乗総和可能な複素数列の空間 ℓ² とは、各項が複素数の無限数列

(c1,c2,c3,…){displaystyle (c_{1},c_{2},c_{3},dots )}

で、条件

|c1|2+|c2|2+|c3|2+⋯<∞{displaystyle |c_{1}|^{2}+|c_{2}|^{2}+|c_{3}|^{2}+cdots <infty }

を満たすもの全体からなる集合（に、項ごとの和、スカラー倍、標準内積を入れたもの）である。この空間には標準的な正規直交基底

e1=(1,0,0,…)e2=(0,1,0,…)⋮{displaystyle {begin{aligned}e_{1}&=(1,0,0,dots )\e_{2}&=(0,1,0,dots )\&quad vdots end{aligned}}}

が存在する。より一般に、任意の集合 B に対して、B 上の自乗総和可能数列の成す空間 ℓ²(B) が

ℓ2(B)={x:B→C |∑b∈B|x(b)|2<∞}{displaystyle ell ^{2}(B)=left{xcolon Bto mathbb {C} left|quad sum _{bin B}|x(b)|^{2}<infty right.right}}

で定義される。ただし B 上の総和というのを、ここでは

∑b∈B|x(b)|2=sup∑n=1N|x(bn)|2{displaystyle sum _{bin B}|x(b)|^{2}=sup sum _{n=1}^{N}|x(b_{n})|^{2}}

で定める（上限は B の有限部分空間すべてに亘って取る）。このようにすると、この和が有限であるところの ℓ²(B) の各元は、可算個の例外を除いた全ての項が 0 になることがわかる。ℓ²(B) の任意の元 x, y に対して、

⟨x,y⟩=∑b∈Bx(b)y(b)¯{displaystyle langle x,yrangle =sum _{bin B}x(b){overline {y(b)}}}

と内積を定めれば、この空間は実際にヒルベルト空間となる。右辺の和は、0 でない項が高々可算個しかないから意味を持ち、またコーシー・シュヴァルツの不等式によって無条件収束であることがわかる。

ℓ²(B) の正規直交基底の一つは、

eb(b′)={1if b=b′0otherwise.{displaystyle e_{b}(b')={begin{cases}1&{text{if }}b=b'\0&{text{otherwise.}}end{cases}}}

で与えられる B で添字付けられた族によって与えられる。

ベッセルの不等式とパーセヴァルの公式

H の有限正規直交系 ƒ₁, …, ƒ_n と H の任意のベクトル x に対して

y=∑j=1n⟨x,fj⟩fj{displaystyle y=sum _{j=1}^{n}langle x,f_{j}rangle f_{j}}

と置くと、各 k = 1, …, n に対して 〈x, ƒ_k〉 = 〈y, ƒ_k〉 が成り立つ。故に x − y は各ƒ_k に直交し、従って x − y は y に直交する。三平方の定理を二度使い

‖x‖2=‖x−y‖2+‖y‖2≥‖y‖2=∑j=1n|⟨x,fj⟩|2{displaystyle |x|^{2}=|x-y|^{2}+|y|^{2}geq |y|^{2}=sum _{j=1}^{n}|langle x,f_{j}rangle |^{2}}

が得られる。さらに {ƒ_i} (i ∈ I) を H の任意の正規直交系とするとき、I の任意の有限部分集合 J に対して先ほどの不等式を適用すれば、（非負実数の任意濃度の族の和の定義に従って）ベッセルの不等式

∑i∈I|⟨x,fi⟩|2≤‖x‖2,x∈H{displaystyle sum _{iin I}|langle x,f_{i}rangle |^{2}leq |x|^{2},quad xin H}

が得られる^[60]。

幾何学的には、ベッセルの不等式が言っているのは、x の f_i たちが生成する部分空間の上への直交射影のノルムは x のノルムを超えないということである。二次元の場合で言えば、これは正三角形の足の長さは斜辺の長さを越えないということになる。

ベッセルの不等式はからは、より強力なパーシヴァルの等式が得られる。これはベッセルの不等式の不等号を等号に取り替えたものになっている。{e_k}_{k ∈ B} が H の正規直交基底ならば、H の各元 x は

x=∑k∈B⟨x,ek⟩ek{displaystyle x=sum _{kin B}langle x,e_{k}rangle e_{k}}

という形に書くことができる。ベッセルの不等式によって B が非可算の場合にも、このような表示が意味を持ち、可算個の例外を除く各項が 0 に等しいことが保証される。このような和を x のフーリエ展開と呼び、個々の係数 〈x,e_k〉 を x のフーリエ係数と呼ぶ。このとき、パーセヴァルの等式は

‖x‖2=∑k∈B|⟨x,ek⟩|2{displaystyle |x|^{2}=sum _{kin B}|langle x,e_{k}rangle |^{2}}

と書ける。逆に、正規直交系 {e_k} が任意の x においてパーセヴァルの等式を満足するならば、{e_k} は正規直交基底になる。

ヒルベルト次元

ツォルンの補題の帰結として、「任意の」ヒルベルト空間が少なくとも一つの正規直交基底を持つことが分かる。さらに、一つの空間ではどの二つの正規直交基底も必ず同じ濃度を持つことが示されるので、その濃度をしてその空間のヒルベルト次元と呼ぶ^[61] 例えば、B 上の自乗総和可能数列の空間 ℓ²(B) は B で添字づけられる正規直交基底を持つから、そのヒルベルト次元は B の濃度（これは有限な整数かもしれないし、可算あるいは非可算の基数であるかもしれない）である。

パーセヴァルの等式の帰結として、{e_k}_{k ∈ B} が H の正規直交基底ならば、Φ(x) := (〈x, e_k〉)_k∈B で定まる写像 Φ: H → ℓ²(B) はヒルベルト空間の等距同型、即ち、全単射な線型写像であって、H の各元 x, y に対して

⟨Φ(x),Φ(y)⟩ℓ2(B)=⟨x,y⟩H{displaystyle langle Phi (x),Phi (y)rangle _{ell ^{2}(B)}=langle x,yrangle _{H}}

を満たすことがわかる。B の濃度は H のヒルベルト次元に等しい。従って、任意のヒルベルト空間は、適当な集合 B に対する数列空間 ℓ²(B) に等距同型である。

可分ヒルベルト空間

ヒルベルト空間が可分であるための必要十分条件は、それが可算な正規直交基底を持つことである。従って、任意の無限次元可分ヒルベルト空間は ℓ² に等距同型になる。

かつてはヒルベルト空間の定義の中に可分であることを含めることが多かった^[62]。物理学に現れる殆どの空間は可分であったことや、どの無限次元可分ヒルベルト空間も全て互いに同型であったことから、任意の無限次元可分ヒルベルト空間に言及するときは「唯一の (the) ヒルベルト空間」とかあるいは単に「ヒルベルト空間」と呼ぶこともしばしばであった^[63]。場の量子論においてさえ、殆どのヒルベルト空間は事実可分であり、ワイトマンの公理系として明記された。しかし、場の量子論において非可分なヒルベルト空間も重要であるというような反論が時には為された。これは大まかには理論における系が無限個の自由度を持ちうることと（1 より大きい次元を持つ空間の）無限個のテンソル積はどれも非可分であることが理由である^[64]。例えばボソン場は自然に、その因子が空間の各点において調和振動子で表現されるようなテンソル積の元と考えることができる。この観点からは、ボソンの空間は非可分であると見るのが自然である^[64]が、しかし全テンソル積の小さな可分部分空間にしか（その上で可観測量が定義できる）物理的に意味のある場が含まれていない。もう一つの非可分ヒルベルト空間モデルは、空間の非有界領域に存在する無限個の素粒子の状態である。この空間の正規直交基底は素粒子の密度を表すある連続なパラメータによって添字付けられる。これは非可算となりうるから、基底は可算ではない^[64]。

直交補空間と射影作用素

S をヒルベルト空間 H の部分集合として、S に直交するベクトル全体の成す集合

S⊥={x∈H:⟨x,s⟩=0 ∀s∈S}{displaystyle S^{perp }=left{xin H:langle x,srangle =0 forall sin Sright}}

を考える。S^⊥ は H の閉部分空間である（これは内積の連続性と線型性用いて容易に示せる）から、それ自身ヒルベルト空間になる。V が H の閉部分空間のとき、V^⊥ は V の直交補空間と呼ばれる。事実、H の各元 x は x = v + w (v ∈ V, w ∈ V^⊥) なる形に一意的に表すことができる。従って、H は V と V^⊥ との内部直和になっている。

この x を v へ写す線型作用素 P_V: H → H を V の上への直交射影と呼ぶ。H の閉部分空間全体の成す集合と有界自己随伴作用素 P で P² = P を満たすもの全体の成す集合との間に自然な一対一対応が存在する。

定理

直交射影 P_V は H のノルム ≤ 1 なる自己随伴作用素で条件 P2
V = P_V を満足する。さらに任意の自己随伴線型作用素 E で E² = E を満たすものは、E の値域を V として P_V の形に表される。また H の各元 x に対して、P_V(x) は距離 ‖x − v‖ を最小にする V の唯一の元 v になる。

このことから、V の元による x の最適近似であるという P_V(x) の幾何学的解釈が得られる^[65]。

二つの射影 P_U, P_V が互いに直交するとは、P_UP_V = 0 が成り立つときにいう。これは U, V が H の部分空間として直交することと同値である。二つの射影 P_U, P_V の和が再び射影となるのは U と V とが互いに直交するときに限られる。このとき P_U + P_V = P_U+V が成り立つ。合成 P_UP_V は一般には射影にならない。事実、合成が射影となる必要十分条件は二つの射影が可換となることであり、その場合 P_UP_V = P_U∩V が成り立つ。

直交射影 P_V の終域をヒルベルト空間 V へ制限することにより、射影 π: H → V が生じる。これは包含写像 i: V → H に対して

⟨ix,y⟩H=⟨x,πy⟩V(x∈V,y∈H){displaystyle langle ix,yrangle _{H}=langle x,pi yrangle _{V}quad (xin V,yin H)}

を満たすという意味での随伴になっている。零でない閉部分空間の上への射影 P の作用素ノルムは

‖P‖=supx∈H,x≠0‖Px‖‖x‖=1{displaystyle |P|=sup _{xin H, atop xneq 0}{frac {|Px|}{|x|}}=1}

に等しい。従って、ヒルベルト空間の任意の閉部分空間 V は、ノルム 1 で P² = P を満たす適当な作用素 P の像になっている。この適当な射影作用素がとれるという性質はヒルベルト空間を特徴付ける性質である^[66]。即ち、

• 2 より大きな次元のバナッハ空間が（等距的に）ヒルベルト空間となるための必要十分条件は、任意の部分空間 V に対し、その像が V となるようなノルム 1 の作用素 P_V で P2
  V = P_V を満たすものが存在することである。

この結果はヒルベルト空間の距離構造を特徴付けるものだが、位相線型空間としてのヒルベルト空間の構造は補空間の存在の言葉で特徴付けられる^[67]。即ち、

• バナッハ空間 X が何らかのヒルベルト空間に位相線型同型（同相かつ線型同型）であるための必要十分条件は、その任意の閉部分空間 V に対し、閉部分空間 W で X が内部直和 V ⊕ W に一致するようなものが存在することである。

直交補空間については、いくつかのより初等的な事実が成立する。「U ⊂ V ならば V^⊥ ⊆ U^⊥ で、等号成立は V が U の閉包に含まれるとき、かつそのときに限る」という意味で、直交補空間をとる操作は単調写像である。これはハーン・バナッハの定理の特別の場合である。部分空間の閉包は直交補空間の言葉で完全に特徴付けることができる。即ち、V が H の部分空間ならば、V の閉包はV^⊥⊥ に一致する。従って、直交補空間をとる操作は、ヒルベルト空間の部分空間全体の成す半順序集合上のガロワ対応（英語版）になっている。一般に、部分空間の合併の直交補空間は直交補空間の交わりに一致する^[68]。即ち

(∑iVi)⊥=⋂iVi⊥{displaystyle {Big (}sum _{i}V_{i}{Big )}^{perp }=bigcap _{i}V_{i}^{perp }}

が成り立つ。さらに V_i が閉ならば

∑iVi⊥¯=(⋂iVi)⊥{displaystyle {overline {sum _{i}V_{i}^{perp }}}={Big (}bigcap _{i}V_{i}{Big )}^{perp }}

を得る。

スペクトル論

ヒルベルト空間における自己随伴作用素のスペクトル論も広く研究が成されている。これには、実係数の場合の対称行列や複素係数の場合の自己随伴行列の研究と大まかな類似がある^[69]。同様の意味で、自己随伴作用素を適当な直交射影作用素の和（実際には積分）として表す「対角化」もできる。

作用素 T のスペクトル σ(T) とは、T − λ が連続な逆作用素を持たないような複素数 λ 全体の成す集合のことである。T が有界ならば、そのスペクトルは必ずガウス平面内のコンパクト集合で、円板 {|z| ≤ ‖T‖} の内側に入る。T が自己随伴ならばそのスペクトルは実であり、事実として区間 [m,M] に含まれる。ただし、

m=inf‖x‖=1⟨Tx,x⟩,M=sup‖x‖=1⟨Tx,x⟩{displaystyle m=inf _{|x|=1}langle Tx,xrangle ,quad M=sup _{|x|=1}langle Tx,xrangle }

とする。さらに言えば m と M はともに実際にはスペクトルに含まれる。

作用素 T の固有空間は

Hλ=ker⁡(T−λ){displaystyle H_{lambda }=ker(T-lambda )}

で与えられる。有限次元の行列の場合と異なり、T のスペクトルの元は必ずしも固有値にはなるとは限らず、線型作用素 T − λ が逆を持たないときだけである（これは全射ではないから）。作用素のスペクトルの元は一般に「スペクトル値」と呼ばれる。スペクトル値は固有値とは限らないので、スペクトル分解は有限次元の場合よりは扱いが難しいことが多い。

しかし、自己随伴作用素 T のスペクトル論は、さらにコンパクト作用素であるという仮定を加えれば特に簡単な形にすることができる。自己随伴コンパクト作用素のスペクトル論の主張は^[70]

• 自己随伴コンパクト作用素 T は高々可算個のスペクトル値しか持たない。T のスペクトルがガウス平面において集積点を持つ可能性は 0 以外にはない。T の固有空間は H の直交直和
  H=⨁λ∈σ(T)Hλ{displaystyle H=bigoplus _{lambda in sigma (T)}H_{lambda }}
  に分解する。さらに固有空間 H_λ の上への直交射影を E_λ と書けば
  T=∑λ∈σ(T)λEλ{displaystyle T=sum _{lambda in sigma (T)}lambda E_{lambda }}
  と表せる。ただし和は B(H) のノルムに関して収束する。

多くの積分作用素、特にヒルベルト＝シュミット作用素から生じるものはコンパクトであり、この定理は積分方程式論において基本的な役割を果たす。

自己随伴作用素に対する一般のスペクトル論には、無限和というよりもある種の作用素値リーマン・スティルチェス積分が関係してくる^[71]。T に伴う「スペクトル族」には、各実数 λ に対して作用素 (T − λ)⁺ の零空間の上への射影 E_λ が対応している。ただし ⁺ は

A+=12(A2+A){displaystyle A^{+}={frac {1}{2}}({sqrt {A^{2}}}+A)}

で定義される自己随伴作用素の正部分を表す。作用素 E_λ は自己随伴作用素の間に定義される半順序に関して単調増大である。固有値はちょうど跳躍不連続点に対応しており、

T=∫RλdEλ{displaystyle T=int _{mathbb {R} }lambda ,dE_{lambda }}

なるスペクトル論が得られる。右辺の積分はリーマン・スティルチェス積分として理解され、B(H) のノルムに関して収束する。特に、通常のスカラー値積分表現

⟨Tx,y⟩=∫Rλd⟨Eλx,y⟩{displaystyle langle Tx,yrangle =int _{mathbb {R} }lambda ,dlangle E_{lambda }x,yrangle }

が得られる。正規作用素に対してもある程度似たようなスペクトル分解が成立するが、この場合実数でない複素数がスペクトルに含まれるから、作用素値スティルチェス測度 dE_λ は 1 の分解で置き換えられなければならない。

スペクトル法の主な応用はスペクトル写像定理（英語版）で、これにより、積分

f(T)=∫σ(T)f(λ)dEλ{displaystyle f(T)=int _{sigma (T)}f(lambda ),dE_{lambda }}

を作って、自己随伴作用素 T に T のスペクトル上で定義される連続な複素関数を施すことができるようになる。このような連続汎函数計算（英語版）は特に擬微分作用素への応用を持つ^[72]。

「非有界」な自己随伴作用素のスペクトル論は、有界作用素に対するものと比べてさほど難しいわけではない。非有界作用素のスペクトルは有界作用素に対するのと全く同じやり方で定義される。つまり、λ がスペクトル値となるのはレゾルベント作用素

Rλ=(T−λ)−1{displaystyle R_{lambda }=(T-lambda )^{-1}}

が連続作用素として定義されないときである。T の随伴性から、やはりスペクトルが実であることが保証される。従って、非有界作用素に特有な議論の本質の部分は、λ が実でないようなレゾルベント R_λ を見るところにある。このレゾルベントは有界正規作用素で、これをスペクトル表現したものを使って T 自身のスペクトル表現が得られる。同様の方法論で、例えばラプラス作用素のスペクトルも調べられる。作用素を直接扱うよりも、それに付随するリースポテンシャルやベッセルポテンシャル（英語版）のようなレゾルベントを見るのである。

非有界自己随伴作用素の場合に成立するスペクトル定理は以下のようなものである^[73]。

ヒルベルト空間 H 上稠密に定義された自己随伴作用素 T が与えられたとき、R のボレル集合族上で定義された 1 の分解 E が一意に対応して

⟨Tx,y⟩=∫RλdEx,y(λ)(x∈D(T),y∈H){displaystyle langle Tx,yrangle =int _{mathbb {R} }lambda ,dE_{x,y}(lambda )quad (xin D(T),yin H)}

を満たす。スペクトル測度 E は T のスペクトル上に集中する。

非有界正規作用素に対するスペクトル定理も存在する。

関連項目

• 対称性 (物理学)


• ヒルベルトC*-加群（英語版）


• ヒルベルト代数（ドイツ語版）


• ヒルベルト多様体（英語版）


• 艤装ヒルベルト空間（英語版）


• 作用素論


• アダマール空間（英語版）

注記

参考文献

• 日本数学会 『岩波数学辞典（第3版）』 岩波書店、1985年。ISBN 4000800167
  

外部リンク

• Weisstein, Eric W. "Hilbert space". MathWorld（英語）. CS1 maint: Multiple names: authors list


• 
  245B, notes 5: Hilbert spaces by Terence Tao